The quantity
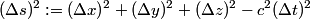 is a Lorentz invariant, meaning that it is the same in any reference frame. We choose as our two events the two flashes of light. We use unprimed variables for the frame of observer 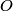 and primed variables for the frame of observer and primed variables for the frame of observer 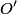 . . 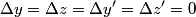 , so , so 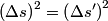 implies that implies that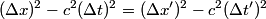 Now, 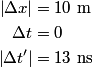 so, 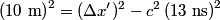 Solving for 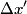 gives gives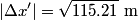 From the Lorentz transformation equations, 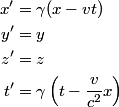 we also have that 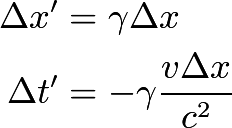 Diving the second equation by the first equation gives or Plugging in 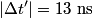 and and 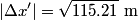 gives gives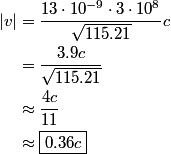 Therefore, answer (C) is correct. |